![[asy]
size(10cm);
import olympiad;
import geometry;
pair A = dir(119);
pair A_prime = -A;
pair E = reflect((0,0), dir(90)) * A_prime;
pair S = dir(90);
pair D = 0.6*E + 0.4*A;
pair B = 2 * foot((0,0), D, S) - S;
pair P = 2 * foot((0,0), A_prime, D) - A_prime;
pair Q = reflect((0,0), (P+A_prime)/2) * S;
pair M = -S;
pair X = extension(E,Q,S,D);
pair Y = extension(P,Q,A,M);
pair L = extension(D+E-A_prime, D, B,E);
fill(X--M--Q--cycle, paleblue);
fill(A--P--S--cycle, paleblue);
draw(unitcircle, linewidth(1));
draw(S--X, red+linewidth(1.2));
draw(P--A_prime, linewidth(0.8));
draw(circle(B,D,P), linewidth(0.8));
draw(P--Q, linewidth(0.8));
draw(X--M--Q--cycle, blue+linewidth(0.8));
draw(A--P--S--cycle, blue+linewidth(0.8));
draw(A--M, linewidth(0.8));
draw(A--E--A_prime, gray+linewidth(0.7));
draw(S--M, gray+linewidth(0.7));
draw(D--L, gray+linewidth(0.7));
dot("$A$", A, dir(118));
dot("$A'$", A_prime, dir(-62));
dot("$E$", E, dir(-84));
dot("$S$", S, dir(89));
dot("$D$", D, dir(16));
dot("$B$", B, dir(-4));
dot("$P$", P, dir(133));
dot("$Q$", Q, dir(17));
dot("$M$", M, dir(-82));
dot("$X$", X, dir(-139));
dot("$Y$", Y, dir(143));
dot("$L$", L, dir(165));
[/asy]](https://latex.artofproblemsolving.com/b/5/b/b5b3a7a42bfd5da332a8282ef2402a6997a5a690.png)
Let
- Since
 , we get that
, we get that  are collinear.
are collinear. - Pascal on
 gives
gives  ,
,  , and
, and  are collinear.
are collinear. - We have
 so
so  . Thus,
. Thus,  and
and  are homothetic at center
are homothetic at center  , so
, so  are collinear.
are collinear.
Hence, ![]() are collinear.
are collinear. ![]() clearly lies on this line, done.
clearly lies on this line, done.
Solution 2
|
Problem 2.
Let proposed by Tiago Mourão and Nuno Arala, Colombia Solution 1
![[asy]
size(10cm);
import olympiad;
import geometry;
pair A = dir(119);
pair A_prime = -A;
pair E = reflect((0,0), dir(90)) * A_prime;
pair S = dir(90);
pair D = 0.6*E + 0.4*A;
pair B = 2 * foot((0,0), D, S) - S;
pair P = 2 * foot((0,0), A_prime, D) - A_prime;
pair Q = reflect((0,0), (P+A_prime)/2) * S;
pair M = -S;
pair X = extension(E,Q,S,D);
pair Y = extension(P,Q,A,M);
pair L = extension(D+E-A_prime, D, B,E);
fill(X--M--Q--cycle, paleblue);
fill(A--P--S--cycle, paleblue);
draw(unitcircle, linewidth(1));
draw(S--X, red+linewidth(1.2));
draw(P--A_prime, linewidth(0.8));
draw(circle(B,D,P), linewidth(0.8));
draw(P--Q, linewidth(0.8));
draw(X--M--Q--cycle, blue+linewidth(0.8));
draw(A--P--S--cycle, blue+linewidth(0.8));
draw(A--M, linewidth(0.8));
draw(A--E--A_prime, gray+linewidth(0.7));
draw(S--M, gray+linewidth(0.7));
draw(D--L, gray+linewidth(0.7));
dot("$A$", A, dir(118));
dot("$A'$", A_prime, dir(-62));
dot("$E$", E, dir(-84));
dot("$S$", S, dir(89));
dot("$D$", D, dir(16));
dot("$B$", B, dir(-4));
dot("$P$", P, dir(133));
dot("$Q$", Q, dir(17));
dot("$M$", M, dir(-82));
dot("$X$", X, dir(-139));
dot("$Y$", Y, dir(143));
dot("$L$", L, dir(165));
[/asy]](https://latex.artofproblemsolving.com/b/5/b/b5b3a7a42bfd5da332a8282ef2402a6997a5a690.png) Let
Hence, Solution 2 Let
 the intersection of the interior bisector of the angle the intersection of the interior bisector of the angle  with with  and let It and let It  be  Additionally Additionally  So   We it suffices to show that  It is sufficient that is  But it is true that  So finally it is sufficient    Therefore from 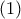 and and  it is sufficient n.d.o: it is sufficient n.d.o:  which is direct. The proof is complete.
|
