Problem 5.
    Let $n$ be a positive integer. A Japanese triangle consists of $1 + 2 + · · · + n$ circles arranged in an equilateral triangular shape such that for each $i = 1, 2, . . . , n$, the $i^{th}$ row contains exactly $i$ circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of $n$ circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with $n = 6$, along with a ninja path in that triangle containing two red circles.

 p5img

In terms of $n$, find the greatest $k$ such that in each Japanese triangle there is a ninja path containing at least $k$ red circles.

proposed by Merlijn Staps, Netherlands

Solution 1
 
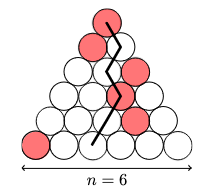
   The answer is $k = \lfloor \log_2 n \rfloor + 1$. To prove that one can't do better, note that it suffices to find a construction for $n = 2^m-1$ that has no path with more than $m$ circles. This is doable by placing the red cells "diagonally" such that no path intersects more than one red cell in rows $1$, $2$, $3$ through $4$, ..., $2^{m-1}$ to $2^m - 1$. An example with $m = 4$ is shown below:

[asy] unitsize(5mm); for (int i = 1; i < 2; ++i) { int j = 2*(i-1); fill(shift(i*dir(240)+j*dir(0))*scale(0.5)*unitcircle,lightred); } for (int i = 2; i < 4; ++i) { int j = 2*(i-2); fill(shift(i*dir(240)+j*dir(0))*scale(0.5)*unitcircle,lightred); } for (int i = 4; i < 8; ++i) { int j = 2*(i-4); fill(shift(i*dir(240)+j*dir(0))*scale(0.5)*unitcircle,lightred); } for (int i = 8; i < 16; ++i) { int j = 2*(i-8); fill(shift(i*dir(240)+j*dir(0))*scale(0.5)*unitcircle,lightred); } for (int i = 1; i < 16; ++i) { for (int j = 0; j < i; ++j) { draw(shift(i*dir(240)+j*dir(0))*scale(0.5)*unitcircle); } } [/asy]


Now we show that $k = \lfloor \log_2 n \rfloor + 1$ is always achievable. To do this, for $1 \leq j \leq i \leq n$, let $a_{i,j}$ be the maximum number of red circles in any path starting from the $j$th circle in the $i$th row and going to the bottom of the triangle. We have the recurrence

\[a_{i,j} = \max\{a_{i+1,j}, a_{i+1,j+1}\} + \begin{cases*} 1 & the $j$th circle in the $i$th row is colored \\ 0 & else \end{cases*}\]
and we wish to show that $a_{1,1} \geq \lfloor \log_2 n\rfloor + 1$.

To do this, our main claim is that
\[\sum_{j=1}^{i} 2^{a_{i,j}} \geq \sum_{j=1}^{i+1} 2^{a_{i+1,j}}\]
for all $i$. This will finish, since we can compute that $\sum_{j=1}^{n} 2^{a_{n,j}} = n+1$, and chaining together these inequalities shows that $2^{a_{1,1}} \geq n+ 1$.

To prove the inequality, pick a specific $i$. For a given $b$, the number of $j$ with $a_{i+1,j} < b$ is strictly greater than the number of $j$ with $\max\{a_{i+1,j}, a_{i+1,j+1}\} < b$, unless the former quantity is zero. Therefore
\begin{align*} \MoveEqLeft \sum_{j=1}^{i+1} 2^{a_{i+1,j}} -\sum_{j=1}^{i} 2^{\max\{a_{i+1,j}, a_{i+1,j+1}\}} \\ & = 1 + \sum_{b=1}^\infty 2^{b-1} (1+\lvert \{ j \mid \max\{a_{i+1,j}, a_{i+1,j+1}\} < b\}\rvert- \lvert \{ j \mid a_{i+1,j} < b\}\rvert) \\ &\leq 1 + \sum_{b = 1}^{\min_j \{a_{i+1,j}\}} 2^{b-1} \\ &= 2^{\min_j \{a_{i+1,j}\}}. \end{align*}
On the other hand, if $j^*$ is the location of the colored circle in row $i$,
\[ \sum_{j=1}^{i} 2^{a_{i,j}} -\sum_{j=1}^{i} 2^{\max\{a_{i+1,j}, a_{i+1,j+1}\}} = 2^{\max\{a_{i+1,j^*}, a_{i+1,j^*+1}\}} \geq 2^{\min_j \{a_{i+1,j}\}}.\]
Subtracting these two inequalities yields the claim.

Solution 2
 
The answer is $\lfloor \log_2(n) \rfloor + 1$.

Proof that $\lfloor \log_2(n) \rfloor + 1$ is achievable.

Consider the following process. Start with an array composed of $n + 1$ zeroes. At any point, if the current array is $[a_1, a_2, \dots, a_k]$, replace it with the $k - 1$ element array

\[[b_1, b_2, \dots, b_{k - 1}] = [\max(a_1, a_2), \max(a_2, a_3), \dots, \max(a_{k - 1}, a_k)]\]
Finally, if the row with $k - 1$ circles has a red circle at position $i$, increase $b_i$ by one. It is straightforward to verify that at any point our $k$-element array gives, for each circle in the row with $k$ circles, the maximum number of red circles that can be visited starting from said circle. For any array consider the quantity $f(a_1, a_2, \dots, a_n) = 2^{a_1} + 2^{a_2} + \dots + 2^{a_n}$.

Main claim. $f(b_1, b_2, \dots, b_{k - 1}) \ge f(a_1, a_2, \dots, a_k)$.

Proof. Let $i$ be such that $a_i = \min(a_1, a_2, \dots, a_k)$. Then we have

\begin{align*} \max(a_1, a_2) &\ge a_1 \quad &\max(a_i, a_{i + 1}) &\ge a_{i + 1} \\ \max(a_2, a_3) &\ge a_2 \quad &\max(a_{i + 1}, a_{i + 2}) &\ge a_{i + 2} \\ &\vdots \quad &&\vdots \\ \max(a_{i - 1}, a_i) &\ge a_{i - 1} \quad &\max(a_{k - 1}, a_k) &\ge a_k \end{align*}
So before adding $1$ to any element, the value of $f$ is at least $2^{a_1} + 2^{a_2} + \dots + 2^{a_{i - 1}} + 2^{a_{i + 1}} + 2^{a_{i + 2}} + \dots + 2^{a_n} = f(a_1, \dots, a_k) - 2^{a_i}$. After adding $1$ to say, $a_j$, the value of $f$ increases by $2^{a_j}$and therefore

\[f(b_1, \dots, b_{k - 1}) \ge f(a_1, \dots, a_k) - 2^{a_i} + 2^{a_j} \ge f(a_1, \dots, a_k)\]
Since $a_i$ was chosen to be minimal. This proves the claim.

Initially we have $f(0, 0, \dots, 0) = n + 1$ and at the end we have a single number $m$. Therefore $2^m \ge n + 1$ and $m \ge \lfloor \log_2 n \rfloor + 1$ as desired.

Proof that $\lfloor \log_2(n) \rfloor + 1$ is the best possible.

It suffices to exhibit a construction with $n = 2^k - 1$ rows in which at most $k$ red circles can be achieved, then prefixes of the triangle provide constructions for other $n$. For each red circle consider drawing the two diagonals parallel to the non-base sides of the triangles and recording which circles on the bottom row they touch. These form an interval of length $\ell$ where $\ell$ is the number of the row counting from the bottom. For the example in the statement we get the intervals $\{[1, 6], [1, 5], [3, 6], [3, 5], [4, 5], [1, 1]\}$. Notice that the intervals uniquely determine the circles, and that we can visit circle $A$ after circle $B$ if and only if the interval corresponding to $A$ contains the interval corresponding to $B$, therefore it suffices to give a collection of intervals of sizes $1, 2, \dots, 2^k - 1$ such that no $k + 1$ of them are nested. Consider now the collection

\[ \begin{matrix} [1, 1] & [2, 3] & [3, 5] & \dots & [2^{k - 1}, 2^k - 1] \\ [1, 2^{k - 1} + 1] & [2, 2^{k - 1} + 3] & [3, 2^{k - 1} + 5] & \dots & [2^{k - 2}, 2^k - 1] \\ [1, 2^{k - 1} + 2^{k - 2} + 1] & [2, 2^{k - 1} + 2^{k - 2} + 3] & [3, 2^{k - 1} + 2^{k - 2} + 5] & \dots & [2^{k - 3}, 2^k - 1] \\ \vdots & \vdots & \vdots & & \vdots \\ [1, 2^{k - 1} + 2^{k - 2} + \dots + 2 + 1] \end{matrix} \]
We can verify that this arrangement contains all lengths of intervals from $1$ to $2^k - 1$ going from left to right, top to bottom. Moreover, no two intervals in the same row contain each other, and therefore any sequence of nested intervals contains at most $k$ of them (one from each row), as desired.