IMO 2023 | PROBLEM 6 - SOLUTION - 9 July 2023

Problem 6.
Let $ABC$ be an equilateral triangle. Let $A_1,B_1,C_1$ be interior points of $ABC$ such that $BA_1=A_1C$ , $CB_1=B_1A$ , $AC_1=C_1B$ , and
$\angle BA_1C+\angle CB_1A+\angle AC_1B=480^\circ$
Let $BC_1$ and $CB_1$ meet at $A_2,$ let $CA_1$ and $AC_1$ meet at $B_2,$ and let $AB_1$ and $BA_1$ meet at $C_2.$
Prove that if triangle $A_1B_1C_1$ is scalene, then the three circumcircles of triangles $AA_1A_2, BB_1B_2$ and $CC_1C_2$ all pass through two common points.

(Note: a scalene triangle is one where no two sides have equal length.)

proposed by Ankan Bhattacharya , USA

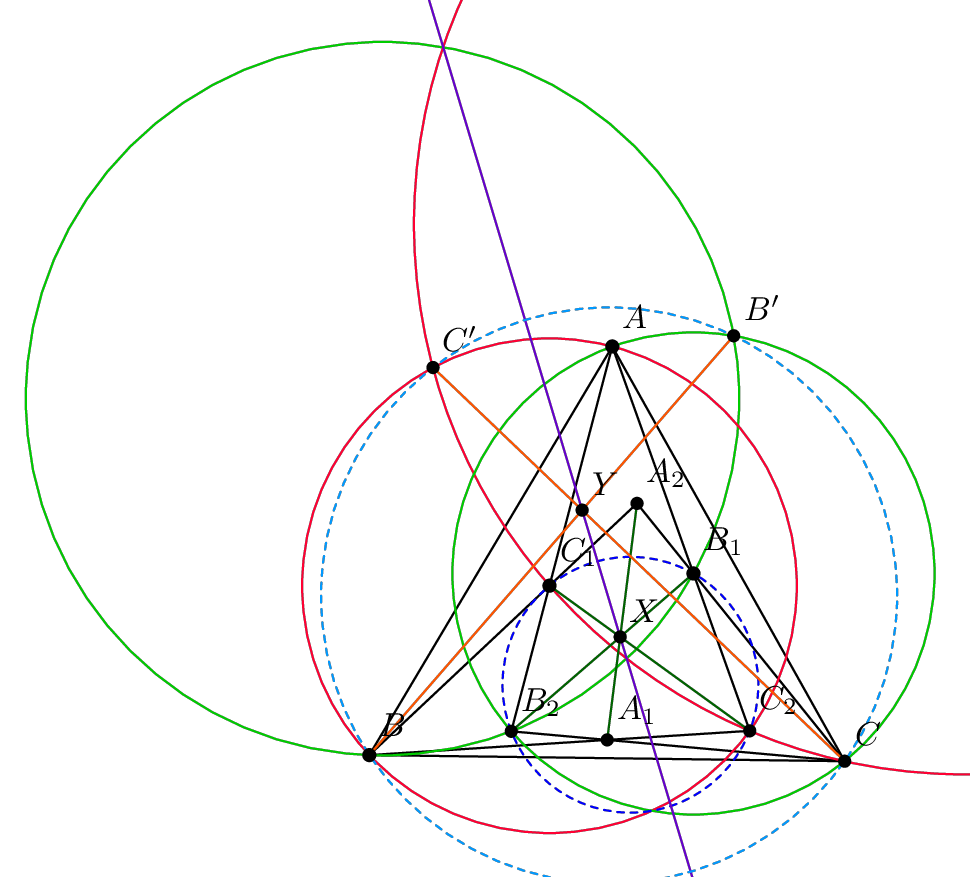
Solution 1

Let $a=\angle A_1BC$ , $b=\angle B_1CA$ , and $c=\angle C_1AB$ , so the condition becomes $a+b+c=30^\circ$ . Note that $\angle BA_2C=60^\circ+b+c=90^\circ-a$ , so $A_1$ is the circumcenter of $BA_2C$ . Similarly, $B_1$ and $C_1$ are the circumcenters of $CB_2A$ and $AC_2B$ . Furthermore, $\angle B_1C_2C_1=90^\circ-\angle ABC_2=a+30^\circ=90^\circ-\angle ACB_2=\angle B_1B_2C_1$ . Thus, $B_1C_1B_2C_2$ is cyclic. Similarly, $C_1A_1C_2A_2$ and $A_1B_1A_2B_2$ are cyclic. Let $\omega_A$ , $\omega_B$ , and $\omega_C$ be the circumcircles of $B_1C_1B_2C_2$ , $C_1A_1C_2A_2$ , and $A_1B_1A_2B_2$ . As $\angle A_2B_1C_2+\angle C_2A_1B_2+\angle B_2C_1A_2=480^\circ$ , we have that $A_2B_1C_2A_1B_2C_2$ is not cyclic and $\omega_A$ , $\omega_B$ , and $\omega_C$ are distinct. By the radical axis theorem, $A_1A_2$ , $B_1B_2$ , and $C_1C_2$ then concur at a point $X$ .

Let $p(K,\omega)$ denote the power of point $K$ to circle $\omega$ . We now compute $\frac{p(A,\omega_B)}{p(A,\omega_C)}$ . Let $\omega_B$ meet $AC_1$ at $D$ and $\omega_C$ meet $AB_1$ at $E$ . We have that $\angle A_1AD=30^\circ-c$ and $\angle A_1DC_1=\angle A_1A_2C_1=90^\circ-\angle S_1CB=30^\circ+b$ , so $\angle AA_1D=b+c$ . Similarly, $\angle A_1AE=30^\circ-b$ , $\angle A_1EB_1=30^\circ+c$ , and $\angle AA_1E=b+c$ . It follows by the law of sines on triangles $AA_1D$ and $AA_1E$ that $\frac{AD}{AE}=\frac{\sin(30^\circ+c)}{\sin(30^\circ+b)}$ . Thus, $\frac{p(A,\omega_B)}{p(A,\omega_C)}=\frac{AC_1}{AB_1}\cdot\frac{\sin(30^\circ+c)}{\sin(30^\circ+b)}$ .
By computing the analogous expressions for the other vertices, we conclude that
$\frac{p(A,\omega_B)}{p(A,\omega_C)}\cdot\frac{p(B,\omega_C)}{p(B,\omega_A)}\cdot\frac{p(C,\omega_A)}{p(C,\omega_B)}=1$ .

To conclude, recall the coaxial lemma: given two circles $\omega_1$ and $\omega_2$ and a constant $c$ , the locus of points $K$ for which $\frac{p(K,\omega_1)}{p(K,\omega_2)}=c$ is a circle coaxial to $\omega_1$ and $\omega_2$ . Hence, the circumcircle of $AA_1A_2$ is the locus of points $K$ with $\frac{p(K,\omega_B)}{p(K,\omega_C)}=\frac{p(A,\omega_B)}{p(A,\omega_C)}$ , and the analogous statements hold for the other vertices. The angle condition implies that segments $AA_1$ , $BB_1$ , and $CC_1$ intersect, so the circumcircles of $AA_1A_2$ , $BB_1B_2$ , and $CC_1C_2$ pairwise intersect at two points. It follows that the circumcircles of $BB_1B_2$ and $CC_1C_2$ intersect at points $P_1$ and $P_2$ satisfying $\frac{p(P_i,\omega_C)}{p(P_i,\omega_A)}=\frac{p(B,\omega_C)}{p(B,\omega_A)}$ and $\frac{p(P_i,\omega_A)}{p(P_i,\omega_B)}=\frac{p(C,\omega_A)}{p(B,\omega_B)}$ for $i=1,2$ . But this then implies that $\frac{p(P_i,\omega_B)}{p(P_i,\omega_C)}=\frac{p(A,\omega_B)}{p(A,\omega_C)}$ for $i=1,2$ , so $P_1$ and $P_2$ both lie on the circumcircle of $AA_1A_2$ , as desired.

Solution 2

Let $\omega_A$ be $(AA_1A_2)$ . Let $f_A(X)$ be the power of an arbitrary point $X$ with respect to $\omega_A$ . Let $\alpha = \angle A_1BC = \angle A_1CB$ . Define $\omega_B,\omega_C$ , $f_B,f_C$ and $\beta,\gamma$ similarly. The angle condition becomes $\alpha+\beta+\gamma=30$ . An angle chase gives that $\angle BA_2C = 60^\circ+\beta+\gamma=90^\circ-\alpha=\frac{1}{2}\angle BA_1C,$ so $A_1$ is the center of $(BA_2C)$ . We then further have $\angle AA_1A_2 = \angle A_2BC - \angle A_2CB = \beta-\gamma$ .

We now compute each of $f_A,f_B,f_C$ evaluated at each of $A,B,C$ . It's direct that $f_A(A)=0$ . It suffices to compute $f_A(B)$ as the remaining formulas follow from symmetry. Let $\omega_A$ meet $AB$ at $T$ . We have $\angle BTA_2 = \angle AA_1A_2 = \beta - \gamma.$ By LOS on $BTA_2$ then $BA_2C$ ,
$f_A(B) = BT \cdot BA = \left(BA_2 \cdot \frac{\sin \angle BA_2 T}{\sin \angle BTA_2}\right) BA =\left( BC \cdot \frac{\sin(BCA_2)}{\sin(BA_2C)} \cdot \frac{\sin( BA_2 T)}{\sin (BTA_2)} \right) BA =s^2 \frac{\sin(60^\circ-\beta)\sin(180^\circ-\beta)}{\sin(90^\circ+\alpha)\sin(\beta-\gamma)},$ where $s$ is the side length of $ABC$ . Now we have all the powers!! The key claim that we've been building up to is the following:

Lemma: If $p=\sin(90^\circ+\alpha) \sin(\beta-\gamma)$ , and $q,r$ are defined similarly, then we have $p+q+r=0$ and $pf_A(X)+qf_B(X)+rf_C(X)=0$ .

Proof: If we write any of the functions $f$ in coordinates, it's $x^2+y^2$ plus some linear equation. It's straightforward to check that $p+q+r=0$ (note $p=\cos(\alpha)\sin(\beta)\cos(\gamma)-\cos(\alpha)\cos(\beta)\sin(\gamma)$ ), so $pf_A(X)+qf_B(X)+rf_C(X)$ is a linear function. Our previous power of a point computation gives $pf_A(X)+qf_B(X)+rf_C(X)=0$ when $X$ is any of $A$ , $B$ , or $C$ . The only linear function that's zero at three noncollinear points is the zero function, so $pf_A(X)+qf_B(X)+rf_C(X)=0$ for all $X$ . $\blacksquare$

Now, $f_A-f_B$ is the linear equation of the radical axis of $\omega_A$ and $\omega_B$ . We also have the analogous property for $f_A-f_C$ . But we also have $q(f_A-f_B)=-r(f_A-f_C)$ , so these are the same line, as desired.

Solution 3

Let $\angle A_1BC=\alpha, \angle B_1AC=\beta, \angle C_1AB=\gamma$ ; the condition rewrites as $\alpha+\beta+\gamma=270^{o}-240^{o}=30^{o}$ . Firstly, we will make use of the angle condition:

$\textbf{Claim 1.}$ $A_1$ is circumcenter of $(BA_2C)$

$\textbf{Proof.}$ We have that $\angle BA_2C=60^{o}+\beta+\gamma=90^{o}-\alpha=\frac{\angle BA_1C}{2}$ and $A_1$ lies on the perpendicular bisector of $BC$ , so the conclusion follows. $\blacksquare$

We have to find two points having equal powers with respect to the circles $(AA_1A_2)$ , $(BB_1B_2)$ and $(CC_1C_2)$ . We will first show that one of them is the concurrency point of $A_1A_2, B_1B_2, C_1C_2$ . This claim is sufficient to prove the result:

$\textbf{Claim 2.}$ $B_1C_1B_2C_2$ is cyclic.

$\textbf{Proof.}$ We have $\angle B_2B_1C_2=\angle (B_1B_2, AC)-\beta=\angle B_2AC+\angle AB_2B_1-\beta=60^{o}-\gamma+90^{o}-\angle ACB_2-\beta=60^{o}-\gamma-\beta+90^{o}-(60^{o}-\alpha)=90^{o}-\gamma-\beta+\alpha=2\alpha+60^{o}$ and similarly $\angle B_2C_1C_2=2\alpha+60^{o}$ . $\blacksquare$

Let $(AA_1A_2) \cap (BA_2C)=A'$ and define $B', C'$ similarly. We will prove that $BC'B'C$ is cyclic, which will imply that $AA', BB', CC'$ concur at a point having equal powers to the three circles, which will finish the problem.

$\textbf{Claim 3.}$ Quadrilateral $BC'B'C$ is cyclic.

$\textbf{Proof.}$ We have that $\angle BB'C=\angle B_2AC+\angle BB_1B_2=60^{o}-\gamma+90^{o}-\angle (B_1B_2, AC) =150^{o}-\gamma-(\angle B_2AC+\angle AB_2B_1)=150^{o}-\gamma-(60^{o}-\gamma+90^{o}-\angle ACB_2)=\angle ACB_2=60^{o}-\alpha$ and similarly $\angle BC'C=60^{o}-\alpha$ , as wanted. $\blacksquare$